Тема исследовательской работы: измерение углового диаметра Луны.
Объект исследования: естественный спутник Земли.
Предмет исследования: данные, полученные в ходе измерения.
Цель исследования: определить диаметр Луны
1. Задачи работы
1. Изучить теоретическую возможность определения углового диаметра Луны с помощью самодельного прибора.
2. Создать собственный прибор для определения углового диаметра Луны
3. С помощью созданного прибора определить угловой диаметр Луны.
Метод исследования: наблюдение естественного спутника Земли с помощью самодельного прибора.
Новизна работы заключается в попытке создания специального прибора для определения углового диаметра Луны.
3. Разработка оптического прибора для определения углового диаметра Луны
Для построения элементарной модели прибора схематически изобразим зависимость углового диаметра Луны от фактического расстояния между поверхностью Земли и центром Луны, а также видимым диаметром её поверхности:
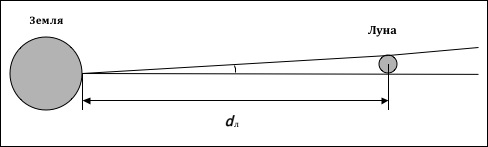
Из приведенной выше схемы видно, что угловой диаметр Луны в радианной мере выражается через отношение её фактического диаметра к расстоянию dл между точкой на поверхности Земли и геометрическим центром Луны.
Исходя из всего вышесказанного, я сконструировал из подручных материалов прибор позволяющий определить значение ρ.
Описание прибора: на две склеенные между собой линейки длиной 50 см. устанавливается специально изготовленный бегунок, состоящий из двух стеклянных пластин 6,5*7см. и двух – 2*7см, склеенных так, чтобы в зазор между двумя пластинами большего размера входили с небольшим трением две склеенные между собой деревянные линейки. К верхней части бегунка приплавливаются две вертикальные пластиковые стойки, в одной из которых нарезается резьба под винт М3. Желательно, чтобы винт ходил с небольшим трением и имел как можно меньший «мёртвый ход». Расстояние между стоиками 6-10мм., высота стоек 10-12мм. Бегунок должен иметь возможность передвигаться по склеенным линейкам с небольшим трением.
Фронтальное сечение измерительного прибора: (полный чертёж прибора приведен в приложении)
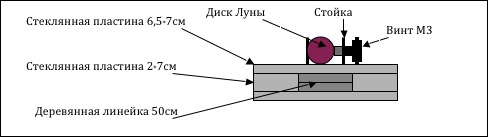
Для этой работы практическое значение будет иметь возможность узнать в миллиметрах расстояние между краем винта и противоположной пластиковой стойкой. Это будет удобно сделать с помощью клина, специально изготовленного из плотного картона:С

1 2 3 4 5 6 7 8 9
Клин. АС = 10 см; ВС = 1 см; АС┴ВС
4. Обоснование математических расчетов данных, полученных от изготовленного прибора
Для обоснования математических расчётов на изготовленном мною приборе удобно рассмотреть рисунок, помещённый на странице -7-, правда, частично преобразованный следующим образом:
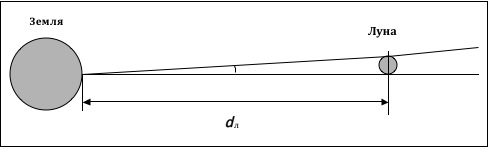
На этом рисунке тачка А, лежащая на поверхности Земли, а также диаметрально противоположные точки В и С, находящиеся на поверхности Луны, образуют прямоугольный треугольник, в котором сторона АС выражает расстояние от поверхности Земли до центра Луны, а катет ВС выражает диаметр последней. Тогда угол А в радианной мере будет выражаться отношением ВС к АС (по аналогии отношения противолежащего катета к прилежащему для тангенса угла А).
В моём приборе, построенном в соответствии с вышеприведенной схемой, сторона АС будет соответствовать расстоянию от края линейки до кончика винта, вкрученного в пластиковую стойку (величина l), а сторона ВС – расстоянию между этим винтом и противоположной стойкой (параметр d), которое замеряется с помощью клина (смотрите нижний рисунок на странице -7-).
В этом случае: LА(рад.) = ; LА(рад.) = ; LА(рад.) = ; ;
Тогда угловой диаметр Луны выражается следующим образом:
ρ=  ; ρ= ; ρ=  (тоже в радианной мере); (тоже в радианной мере);
Таким образом, выразив угловой диаметр Луны – постоянный параметр для этого небесного тела, не будет составлять и особого труда найти и обычный её диаметр, подставив значение dл, выражающее расстояние от поверхности Земли до центра Луны, которое можно найти в любом астрономическом справочнике (оно составляет 3,84*108 м):
D = ρ*dл;
Радиус Луны, таким образом, будет составлять:
R = D/2; R = (ρ*dл)/2.
5. Руководство по использованию изготовленного прибора:
Для определения углового диаметра Луны с помощью изготовленного прибора необходимо правильно выбрать время. Во-первых: это должно быть полнолуние, когда спутник предстает перед Землёй полностью освещённым и представляет собой диск правильной округлой формы, во-вторых: по понятной причине измерение необходимо проводить в безоблачную погоду.
Сначала отодвигаем бегунок от нулевого деления линейки приблизительно на 40 сантиметров. Направляем щель между двумя пластиковыми стойками на диск Луны. И, смотря на щель со стороны нулевого деления (глаз располагаем как можно ближе), ловим диск Луны в прорезь. Если диск Луны свободно помещается в щели, то отодвигаем скобу дальше от нулевого деления линейки или закручиваем винт. Добиваемся такого расположения, при котором диск будет касаться левой стойки и кончика винта. После этого ширину щели измеряем клином. Замеряем расстояние, на котором оказался от нулевого деления линейки кончик винта. Измерения повторяем несколько раз, чтобы найти их среднеарифметическое значение.
Как говорилось выше, ширина щели обозначается через d, а расстояние от нулевого деления линейки до кончика винта – l. Тогда угловой диаметр Луны ρ в радианной мере:
ρ =  . .
6. Вычисление углового диаметра Луны
Измерения мною проводились в количестве трёх раз, но для более точного нахождения параметра ρ необходимо найти среднее арифметическое параметров d и l.
Результаты измерений представлены в таблице:
|
№ измерения
|
d, мм.
|
l, мм.
|
|
I
|
4,5
|
503
|
|
II
|
5,0
|
559
|
|
III
|
4,0
|
447
|
|
Средн. арифм.
|
4,5
|
503
|
Теперь, используя значения d=4,5мм., l=503мм. найдём соответствующее значение ρ:
ρ =  = 0,00895 рад. = 0,00895 рад.
При известном значении углового диаметра Луны не представляет никакого труда вычислить в метрах реальный диаметр Луны, а также её радиус:
D = ρ*dл; dл = 3,84*108 м;
D = 0,00895 рад. * 3,84*108 м = 8,95*10-3рад. * 3,84*108 м = 3,44*106 м.
R = D/2
R = 3,44*106м / 2 = 1,72*106 м.
|